R로 배우는 회귀분석 실습 ( 베이징 미세먼지(PM2.5) 데이터 분석 )

R로 배우는 회귀분석 실습 ( 베이징 미세먼지(PM2.5)  )

   [ 목차 ] 

     분석목적

     데이터개요  

     분석방법  

     R코드   

         - 데이터 불러오기
         - 변수 추출 및 전처리
         - 다중회귀 모델 생성 및 결과 요약
         - 시각화

     결론 및 시사점결론 및 시사점   

 

회귀분석 실습

1. 분석 목적

본 분석의 목적은 베이징 지역의 미세먼지 농도(PM2.5)에 영향을 미치는 기상 요인을 파악하고, 이를 바탕으로 예측 모델을 수립하는 것이다. 이를 위해 미국 대사관의 PM2.5 측정값(PM_US_Post)을 종속 변수로 사용하고, 기온, 이슬점, 기압, 습도, 풍속 등의 기상 데이터를 독립 변수로 사용하여 다중회귀분석을 실시하였다.

 

2. 데이터 개요

• 데이터 출처: Kaggle - Beijing PM2.5 Dataset (2010~2015)
• 총 관측치: 약 50,000건
• 주요 변수 설명:

BeijingPM20100101_20151231.csv

3.03MB

변수명설명

PM_US_Post	PM2.5 농도 (미국 대사관 측정값)
TEMP	기온 (°C)
DEWP	이슬점 (°C)
PRES	기압 (hPa)
HUMI	습도 (%)
Iws	누적 풍속 (m/s)

❗ 바람 방향(cbwd)은 범주형 변수로 이번 분석에서는 제외하였음

 

R을 활용한 당뇨병 데이터 분류

 

3. 분석 방법

• 사용 언어: R
• 분석 기법: 다중선형회귀분석 (lm() 함수)
• 결측값 처리: na.omit()으로 제거
• 시각화: 기본 plot(), ggplot2, pairs() 사용

 

 

4. R코드

 

# 데이터 불러오기
data <- read.csv("BeijingPM20100101_20151231.csv")

---

# 변수 추출 및 전처리
selected_data <- data[, c("TEMP", "DEWP", "PRES", "HUMI", "Iws", "PM_US.Post")]
names(selected_data)[names(selected_data) == "PM_US.Post"] <- "PM_US_Post"

 

selected_data <- na.omit(selected_data)  # 결측값 제거

 

View(selected_data)

---

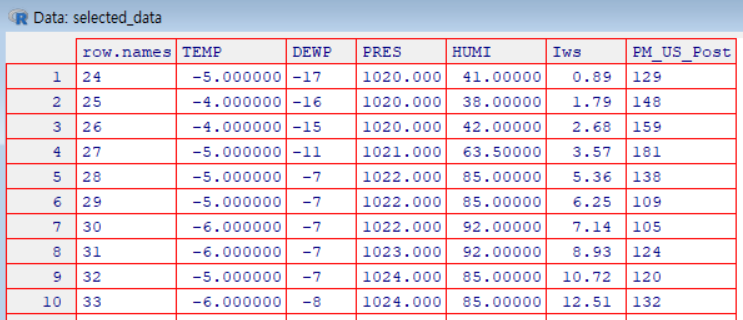
# 다중회귀 모델 생성
model <- lm(PM_US_Post ~ TEMP + DEWP + PRES + HUMI + Iws, data = selected_data)

# 회귀 결과 요약
summary(model)

변수계수유의확률 (p-value)해석

TEMP(기온)	-1.42	< 0.001	기온 증가 시 PM2.5 감소
DEWP(이슬점)	-1.01	< 0.001	이슬점 증가 시 PM2.5 감소
PRES(기압)	-1.46	< 0.001	기압 증가 시 PM2.5 감소
HUMI(습도)	+1.57	< 0.001	습도 증가 시 PM2.5 증가
Iws(풍속)	-0.27	< 0.001	풍속 증가 시 PM2.5 감소

GDP로 보는 대한민국의 변화

# 예측값 계산
predicted <- predict(model)

---

# 시각화 1: 잔차 진단 플롯
par(mfrow = c(2, 2))
plot(model)

 

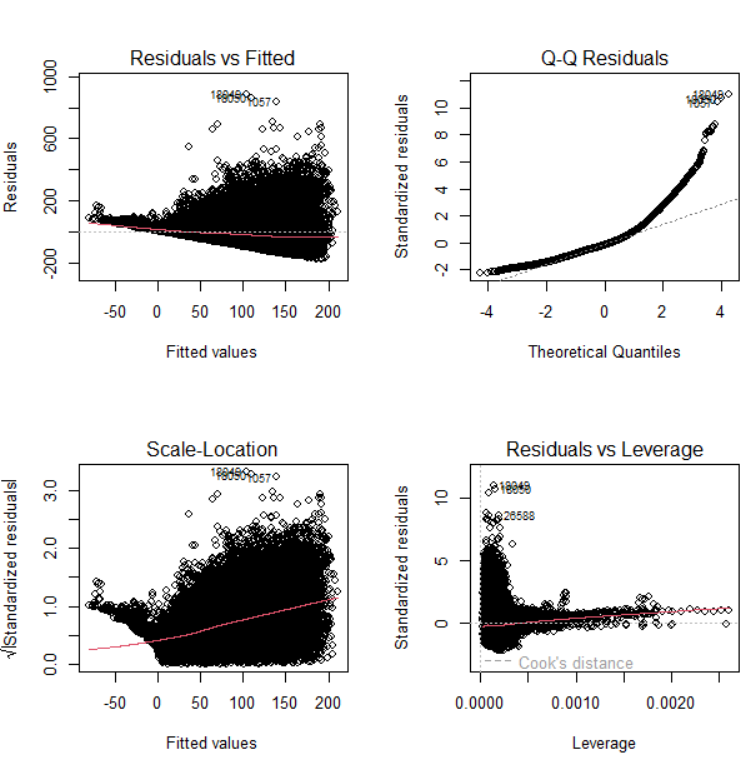
• 잔차가 비교적 일정한 패턴을 보여 선형 회귀의 기본 가정을 대체로 만족함
• 다만, 일부 분산이 큰 영역에서는 이분산성 의심 가능

 

---

국내 인구동향 변화 분석

# 시각화 2: 실제값 vs 예측값
plot(selected_data$PM_US_Post, predicted,
     xlab = "실제 PM2.5", ylab = "예측된 PM2.5",
     main = "실제 vs 예측 PM2.5",
     pch = 20, col = "blue")
abline(0, 1, col = "red", lwd = 2)

 

• 예측값이 실제값과 유사하게 분포하고 있으나, 낮은 PM2.5 구간에서 편차가 큼
• 회귀모델의 정확도는 한계가 있으나, 대략적 경향 파악에는 유용함

---

# 시각화 3: 변수 간 산점도 행렬
pairs(selected_data,
      main = "변수 간 산점도 행렬",
      pch = 19, col = rgb(0, 0, 1, 0.3))

 

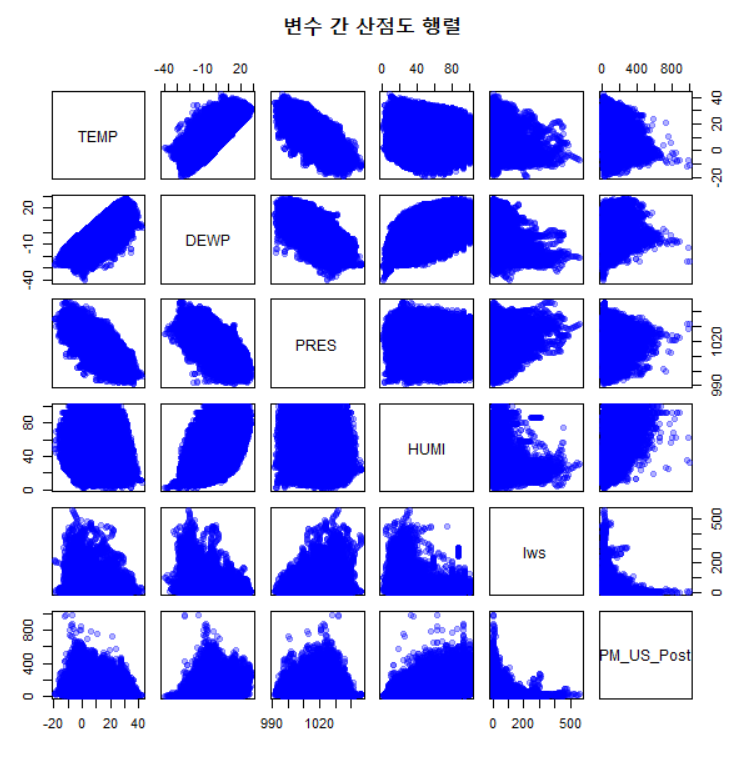
변수들 간 선형 관계가 일부 존재하며, DEWP(이슬점), TEMP(기온), PRES(기압) 등이 서로 연관된 패턴을 보임. 

변수들 간 선형 관계가 일부 존재하며, DEWP(이슬점), TEMP(기온), PRES(기압) 등이 서로 연관된 패턴을 보임

 

R로 알아보는 미국 치안지도

 

5. 결론 및 시사점

• TEMP(기온) , DEWP(이슬점) , PRES(기압) , lws(풍속이) 증가하면 PM2.5 농도는 낮아지는 반면,
  HUMl(습도)는 오히려 증가 요인으로 작용함.
• 회귀 모델의 설명력은 약 22.7%로, 단순 기상 요소만으로는 완벽한 예측이 어려움.
• 향후 바람 방향, 교통량, 산업 활동 등 추가적인 변수를 포함하면 설명력을 높일 수 있음.
• 비선형 기법(Random Forest, XGBoost 등)으로 확장하여 비교분석도 추천됨.

* 추천 후속 작업 :

    - 계절별 회귀 분석

    - 시계열 기반 예측 모델 구축

    - 머신러닝 모델 비교 (회귀 vs 트리 기반 모델)