R로 회귀 모델 만들기 : 주행 속도와 제동 거리
R의 내장 데이터셋인 cars를 활용해 속도(speed)와 제동 거리(dist) 사이의 관계를 분석해 봅시다.
1. 데이터 확인
첫 번째 단계는 데이터의 구조를 살펴보는 것입니다. cars는 R에 기본으로 내장된 데이터셋으로, 두 개의 열로 구성되어 있습니다.
- speed: 자동차의 속도 (단위: mph)
- dist: 해당 속도에서 정지하기까지의 제동 거리 (단위: ft)
이 데이터를 통해 우리는 속도와 제동거리 사이에 어떤 관계가 있는지 분석하게 됩니다.

2. 산점도 그리기


산점도(Scatter plot)는 두 변수 간의 관계를 시각적으로 보여줍니다. 이 그래프를 통해 "속도가 빨라질수록 제동거리가 길어지는구나"라는 패턴을 육안으로 파악할 수 있습니다.
3. 선형 회귀 모델 생성
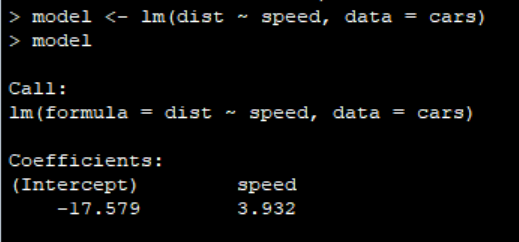
lm() 함수는 선형 모델(linear model)을 만드는 함수입니다.
형식은 lm(종속변수 ~ 독립변수, data=데이터)입니다.
이 경우에는:
- 독립변수(x): speed
- 종속변수(y): dist
출력 결과에서 Coefficients: 아래 값을 보면 모델의 기울기(w)와 절편(b)을 확인할 수 있습니다.
dist = 3.932 * speed - 17.579 : 이게 바로 우리가 만든 회귀식(예측 모델)입니다.
4. 예측하기
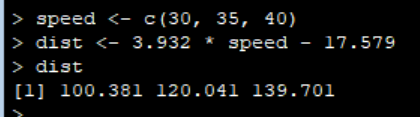
속도가 각각 30, 35, 40일 때 제동거리를 예측해 봅시다.
회귀식을 활용하면 새로운 x 값(speed)에 대해 y 값(dist)을 예측할 수 있어요.
5. 회귀선 그리기
산점도 위에 회귀선을 추가해 추세를 시각화해 보겠습니다.

abline(model)을 사용하면 산점도 위에 회귀선을 그릴 수 있습니다.
이 선은 모델이 예측한 전체적인 추세를 보여줍니다.
- 점들이 이 직선 근처에 모여 있을수록 모델이 데이터를 잘 설명하고 있는 것입니다.

예측값과 실제값이 얼마나 유사한지 비교해 보면

이 단계에서는 모델이 얼마나 정확한지를 확인할 수 있습니다.
- x축: 모델이 예측한 값
- y축: 실제 관측된 값
만약 모든 점이 y = x 직선(빨간 선) 위에 놓여 있다면, 예측값과 실제값이 완전히 일치하는 것입니다.
점들이 이 선 근처에 모여 있다면 모델이 꽤 정확하다고 볼 수 있어요.

6. 마무리
단순 선형 회귀는 매우 직관적이고 실용적인 예측 기법입니다. 두 변수 간의 관계가 직선형일 때, 이를 수학적으로 모델링해 향후 결과를 예측할 수 있게 도와줍니다. 비즈니스, 공학, 데이터 과학, 경제 분야 등 다양한 분야에서 널리 사용되고 있죠.
이번 글에서는 cars 데이터셋을 통해 속도와 제동거리 사이의 관계를 분석하고 예측하는 방법을 실습해 봤습니다.
'IT관련' 카테고리의 다른 글
| 수면 시간과 스트레스가 수면의 질에 어떤 영향을 줄까? ( + R 회귀분석 ) (0) | 2025.04.09 |
|---|---|
| 중선형 회귀모델 , 교육, 평판, 여성 비율로 알아보는 연봉 예측 모델 ( +R코드 ) (0) | 2025.04.07 |
| GDP로 보는 대한민국의 변화 – 경제성장, 출산율, 기대수명의 상관관계( + R코드) (0) | 2025.04.02 |
| 국내 인구동향 변화 분석 (1970~2023) ( + R코드 ) (1) | 2025.04.01 |
| 빅데이터 분석이란? 개념과 활용사례 총정리 (0) | 2025.03.31 |



